2. Binary Search Tree (BST)
- Due date: 11:59pm, 10/27/2024
- TA: Sangyun Kim (sangyun.kim@snu.ac.kr)
Goals
-
Get familiar with C++ programming by implementing simple data structures like BST.
-
Get to know what is
std::unique_ptrand how to use it. -
Learn how to implement the simple and easy binary tree before B-tree assignment.
Preparation
Download the handout tarball, 02-BST.tar.gz and then decompress it.
$ cd ~
$ wget https://compsec.snu.ac.kr/class/data-structure/files/02-BST.tar.gz
Table of contents
BST
Definitions
A BST is a binary tree where nodes are ordered in the following way:
each node contains one element (also known as data)
the elements in the left subtree are less than the element in its parent node
the elements in the right subtree are greater than the element in its parent node
duplicate elements are not allowed.
Types
We will take a look at the types:
template <typename T>
class TreeNode
{
public:
T element;
std::unique_ptr<TreeNode<T>> left;
std::unique_ptr<TreeNode<T>> right;
TreeNode<T>(const T& e)
:element{e}, left{nullptr}, right{nullptr} {}
~TreeNode() {}
};
template <typename T>
class BST
{
public:
std::unique_ptr<TreeNode<T>> root = nullptr;
~BST() {}
bool insert(const T& key);
bool search(const T& key);
bool remove(const T& key);
private:
bool insert(std::unique_ptr<TreeNode<T>>& t, const T& key);
bool search(std::unique_ptr<TreeNode<T>>& t, const T& key);
bool remove(std::unique_ptr<TreeNode<T>>& t, const T& key);
T find_rightmost_key(std::unique_ptr<TreeNode<T>>& t);
};
A BST provides all necessary operations for BST and it also has a
pointer to a root node. Then TreeNode implements each node, which
has two pointers (one for left and the other for the right children)
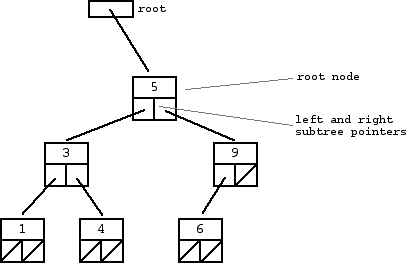
This figure is from http://cslibrary.stanford.edu/110/BinaryTrees.html
Note that a node does not have a pointer to its parent node, and
in this assignement, we will use std::unique_ptr for every pointer pointing TreeNode.
Your goal is to fill in all of the TODO regions.
Insertion
The strategy for insertion is simple. We start at the root and recursively go down the tree searching for a location to insert a new node. The property of BST should be always preserved even after the node insertion.
In this assignment,
if the new node is sucessfully inserted, the function insert(const T& key) returns true, otherwise returns false.
Insertion Example
Suppose you are given a BST like below. If you attempt to insert a new node "8" into the tree:
5 5
/ \ insert(8) / \
3 9 ==> 3 9
/
8
Search
Searching in a BST always starts at the root. We compare a data stored at the root with the element we are searching for (hereafter call this as KEY). If the element of root is the same with KEY, we are done. If the element of root is smaller than KEY, we move on to the left child. Otherwise, move on to the right. The recursive structure of a BST yields a recursive algorithm.
In this assignment,
if KEY exists in BST, the function search(const T& key) returns true, otherwise returns false.
Deletion
Deletion is somewhat more tricky than insertion.
There are several cases to be considered: A node to be deleted (let us call it as KEY)
- is a leaf;
- has only one child;
- has two children.
- is not in a tree;
In this assignment,
if the node is sucessfully deleted, the function remove(const T& key) returns true, otherwise returns false.
Deletion Example
Given a BST, we try to delete a node "8" in the tree:
case 1: is a leaf;
5 5
/ \ remove(8) / \
3 9 ==> 3 9
/
8
The node "8" is a leaf node, so just delete that node.
case 2: has only one child;
Given a BST, we try to delete a node "9" in the tree:
5 5
/ \ remove(9) / \
3 9 ==> 3 8
/
8
The node "9" has only one child, so the procedure of deletion is identical to deleting a node from a linked list - we just bypass that node being deleted.
case 3: has two children.
Given a BST, we try to delete the node "5" in the tree:
5 4
/ \ remove(5) / \
3 9 ==> 3 9
/ \ /
1 4 1
The node "5" has two children, so we first find the max element from its left subtree (let us call it as L_subtree). In this case, the node "4" is max.
We then replace the node "5" with the maximum value, "4". Then delete the node "4" in L_subtree.
case 4: is not in a tree;
In this case, do nothing :)
Submission and Grading
Testing your own programs
In 02-BST directory, you run the following commands to compile your implementation.
$ pwd
/xxx/xxx/xxx/02-BST
$ mkdir build
$ cd build
$ cmake ../
$ make
$ ls tests/BST_test
./test/BST_test
$ ./tests/BST_test
[...]
If you've all done correctly, the output should be like this:
===============================================================================
All tests passed (XX assertions in XX test cases)
Submission
Prepare your submission by executing the script,
prepare-submit.sh.
It creates a compressed tar ball, assign2.tar.gz using your BST.hpp.
$ pwd
/xxx/xxx/xxx/02-BST
$ ./prepare-submit.sh
[*] Remove tar file...
[*] Compress files...
./include/BST.hpp
[*] Successfully Compressed!
[*] Done! You are ready to submit
Option 1: Download from the Remote Server Container
If you are using the container on the kayle server, you can
transfer the assign2.tar.gz file to your local computer
using the scp command:
Open your local terminal (e.g., PowerShell, Bash, etc.)
$ scp -P <port> compsec@kayle.snu.ac.kr:~/02-BST/assign2.tar.gz ./
compsec@kayle.snu.ac.kr's password:
assign2.tar.gz 100% 273 36.8KB/s 00:00
$ ls
assign2.tar.gz
<port>: This is the SSH port used to connect to the container.
Option 2: Download from Your Local Machine’s Container
If you are running the container on your own local machine, use the following scp command to copy the file from the container:
Open your local terminal (e.g., PowerShell, Bash, etc.)
$ scp -P 22222 compsec@localhost:~/02-BST/assign2.tar.gz ./
compsec@localhost's password:
assign2.tar.gz 100% 273 36.8KB/s 00:00
$ ls
assign2.tar.gz
Finally, once you have the assign2.tar.gz file on your local machine, upload it to the eTL.